스택에서는 데이터가 도착하는 순서가 중요하다.
정의: 스택은 삽입과 삭제가 한쪽 끝에서 이루어지는, 순서가 매겨진 리스트이다. 이 끝을 탑이라고 부른다. 제일 마지막에 추가된 항목이 제일 먼저 삭제된다(LIFO, FILO).
스택이 가질 수 있는 두 가지 변화에 대한 특별한 이름이 있다. 스택에 항목이 삽입될 때, 이 것을 푸시(push)라고 부르고, 항목이 스택으로부터 삭제되는 것을 팝(pop)이라고 부른다. 빈 스택으로부터 항목을 팝하려는 것을 언더플로우(underflow)라고 하고, 가득 찬 스택에 푸시하려는 것을 오버플로우(overflow)라고 하는데, 일반적으로 이런 경우는 예외처리한다.
- 스택 ADT
스택의 주요 연산들
push(int data): 데이터를 스택에 넣는다.
int Pop(): 스택에 제일 마지막에 추가된 항목을 스택으로부터 삭제하고 리턴한다.
스택의 보조적 연산들
int Top(): 스택에 마지막에 추가된 항목을 삭제하지 않고 리턴한다.
int Size(): 스택에 저장된 항목의 개수를 리턴한다.
int IsEmptyStack(): 스택에 항목이 저장되어 있는지 아닌지를 확인한다.
int IsFullStack(): 스택이 가득 찼는지 아닌지를 확인한다.
- 스택의 구현
여러 가지 방법들
간단한 배열에 기반한 구현
동적 배열에 기반한 구현
연결 리스트 구현
간단한 배열 구현
이렇게 ADT를 구현할 때는 하나의 배열이 사용된다. 배열에 항목을 왼쪽에서 오른쪽으로 추가하면서 변수 하나를 사용하여 탑 항목의 인덱스를 추적한다.
스택 항목을 저장하는 배열은 가득 찰 수도 있다. 이 경우, 푸시 연산은 '꽉찬 스택 예외'를 발생시킨다. 유사하게 빈 스택으로부터 항목을 삭제하려고 하면 '빈 스택 예외'를 발생시킨다.
public class ArrayStack{
private int top;
private int capacity;
private int[] array;
public ArrayStack() {
capacity = 1;
array = new int[capacity];
top = -1;
}
public boolean isEmpty(){
/* 이 조건이 참이면 1이 리턴하고 아니면 0이 리턴된다. */
return (top == -1);
}
public int isStackFull(){
// 이 조건이 참이면 1이 리턴되고 아니면 0이 리턴된다.
return (top == capacity - 1); //혹은 return (top == array.length);
}
public void push(int data) {
if(isStackFull()) System.out.println("Stack Overflow");
else // 'top'을 증가시키고 데이터를 'top'위치에 저장한다.
array[++top] = data;
}
public int pop(){
if(isEmpty()) { // top == -1은 스택이 비었음을 뜻한다
System.out.println("Stack is Empty");
return 0;
}
else return (array[top--]);
}
public void deleteStack(){
top = -1;
}
}
성능과 한계
성능
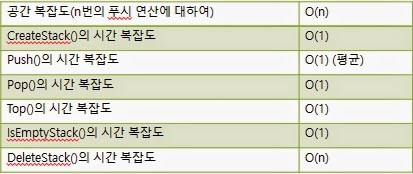
스택 안의 항목의 개수를 n이라고 하자. 이 구현의 스택 연산 복잡도는 다음과 같다.
- 동적 배열 구현
top이라는 인덱스 변수를 써서 스택에 가장 최근에 추가된 항목의 인덱스를 가리키게 했다.
항목을 추가하려면 top인덱스를 증가시키고 새 항목을 그 인덱스 자리에 넣는다. 유사하게 항목을 삭제하려면, top 인덱스의 항목을 취하고 top 인덱스를 감소시킨다. 우리는 top의 값을 -1로 두어 빈 스택을 나타낸다. 여전히 해결해야 할 문제는 고정된 크기의 배열 스택의 모든 항목이 다 찼을 때 처리하는 방법이다.
첫번째 시도
스택이 가득 찰 때마다 배열의 크기를 1씩 증가시키자.
문제점)
이 방식으로 배열 크기를 증가시키는 것은 비용이 너무 크다. 예를 들어 n = 1일 때 새 항목을 푸시하려면 크기가 2인 배열을 만들고 이전 배열의 모든 항목을 새 배열로 복사한 후 맨뒤에 새 항목을 추가해야한다. 또다른 경우로서 n = n-1일 때 새 항목을 푸시하려면, 크기가 n인 새 배열을 만들어 이전 배열의 모든 항목을 새 배열로 복사한 후 맨 뒤에 새 항목을 추가해야 한다. n번의 푸시 이후에 전체 시간 T(n0 (복사 연산의 횟수)은 1 + 2 + ... + n ≒ O(n^2)에 비례한다.
다른 접근 방법: 반복적인 두 배 확장
배열이 가득 차면, 크기가 2배인 새 배열을 만들어 항목들을 복사한다. 이 방법에서는 n개의 항목을 푸시할 때 n(n^2이 아닌)에 비례하는 시간이 걸린다. 처음에 n = 1에서 시작해서, n = 32일 때까지 계속한다고 하자. 즉 1,2,4,8,16일 때 두 배로 만든다는 것이다. 이를 분석하는 다른 방법은, n = 1일 때 새 항목을 추가하려면 현재 배열의 크기를 두 배로 만들고 모든 항목을 이전 배열에서 새 배열로 복사하는 것이다.
n = 1일때 한 번의 복사를 하고, n = 2일 때 두 번의 복사를 하고, n = 4일 때 네 번의 복사를 하는 식이다. n = 32가 될 때면 복사 연산의 총합은 1 + 2 + 4 + 8 + 16 = 31이고, 이것은 대략 2n(32)와 비슷하다. 자세히 관찰하면, 두 배로 만드는 연산을 logn번 하는 것을 알 수 있다. 이제 n번의 푸시 연산에 배열 크기를 두 배로 만드는 것을 logn번 수행하면, logn 항을 갖는다. n번의 푸시 연산의 전체 시간 T(n)은 연산의 횟수에 비례한다.
1 + 2 + 4 + 8 ... + n/4 + n/2 +n = 2n = O(n)
T(n)은 O(n)이고 푸시 연산의 상각 시간은 O(1)이다.
public class DynArrayStack {
private int top;
private int capacity;
private int[] array;
public DynArrayStack() {
capacity =1;
array = new int[capacity];
top = -1;
}
public boolean isEmpty(){
return (top == -1);
}
public int isStackFull(){
return (top == capacity - 1);
}
public void push(int data) {
if(isStackFull())
doubleStack();
array[++top] = data;
}
private void doubleStack(){
int newArray[] = new int[capacity*2];
System.arraycopy(array, 0 ,newArray, 0, capacity);
capacity = capacity*2;
array = newArray;
}
public int pop() {
if(isEmpty()) System.out.println("Stack Overflow");
else return (array[top--]);
}
public void deleteStack() {
top = -1;
}
}
- 성능
연결 리스트 구현
스택을 구현하는 또 다른 방법은 연결 리스트를 사용하는 것이다. 푸시 연산은 리스트의 맨 앞에 항목을 삽입하는 것으로 구현된다. 팝 연산은 리스트 가장 처음 노드를 삭제하는 것으로 구현된다.
public class LLStack extends Stack {
private LLNode headNode;
public LLStack() {
this.headNode = new LLNode(null);
}
public void Push(int data){
if(headNode == null) {
headNode = new LLNode(data);
}else if(headNode.getData() == null){
headNode.setData(data);
}else{
LLNode llNode = new LLNode(data);
llNode.setNext(headNode);
headNode = llNode;
}
}
public int top() {
if(headNode == null) return null;
else return headNode.getData();
}
public int pop(){
if(headNode == null) {
throw new EmptyStackException("Stack empty");
}else{
int data = headNode.getData();
headNode = headNode.getNext();
return data;
}
}
public boolean isEmpty() {
if(headNode == null) return true;
else return false;
}
public void deleteStack(){
headNode = null;
}
}
- 성능
- 각 구현 방법의 비교
점진적 증가 기법과 두 배 확장 기법의 비교
점진적 증가 기법
푸시 연산의 상각 시간은 O(n)이다.
두 배 확장 기법
푸시 연산의 상각 시간이 O(1)이다.
- 배열 구현과 연결 리스트 구현의 비교
배열 구현
연산의 수행에는 일정한 시간이 걸린다.
가끔 비용이 큰 두 배 확장 연산을 수행한다.
(빈 스택으로부터 시작하는) n번의 연산에 상각하는 n에 비례하는 시간이 걸린다.
연결 리스트 구현
부드럽게 커지고 작아진다.
모든 연산에 일정한 시간 O(1)이 걸린다.
모든 연산에 레퍼런스를 다루기 위한 부가적인 공간과 시간이 필요하다.




댓글 없음:
댓글 쓰기